/Konkursy

Zadanie nr 9797060

Dodaj do ulubionych
Dodaj do rozwiązanych

Która z poniższych liczb nie może być wartością wyrażenia 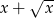√ -- x + x , gdzie x jest liczbą całkowitą?
A) 870 B) 110 C) 90 D) 60 E) 30

Rozwiązanie

Sposób I

Jeżeli podane wyrażenie napiszemy w postaci 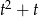t2 + t , gdzie 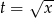√ -- t = x , to łatwo zobaczyć, które z podanych liczb są w tej postaci (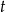t musi być liczbą naturalną).

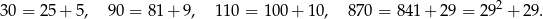
30 = 25 + 5, 90 = 81 + 9, 11 0 = 100 + 10, 8 70 = 841 + 29 = 2 92+ 29 .

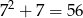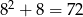Z drugiej strony, 60 nie da się napisać w ten sposób (bo 2 7 + 7 = 56 i 82 + 8 = 7 2 ).

Sposób II

Podobnie jak poprzednio zauważamy, że podane wyrażenie można zapisać jako 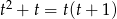t2 + t = t(t+ 1) . Wystarczy teraz zauważyć, że

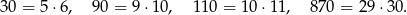
30 = 5⋅6, 90 = 9 ⋅10, 1 10 = 10 ⋅11, 8 70 = 29 ⋅30.

Jednocześnie

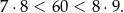
7 ⋅8 < 60 < 8 ⋅9.

Sposób III

Żeby zobaczyć o co chodzi, spróbujmy rozwiązać równanie

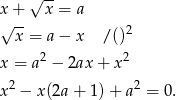
√ -- x + x = a √ -- 2 x = a − x /() x = a2 − 2ax + x 2 2 2 x − x(2a + 1) + a = 0.

A zatem

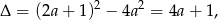
Δ = (2a + 1)2 − 4a2 = 4a + 1,

musi być pełnym kwadratem. Sprawdzając podane liczby, można zauważyć, że 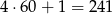4 ⋅60 + 1 = 24 1 nie jest pełnym kwadratem.  
Odpowiedź: D

Wersja PDF