Zadanie nr 2774776

Nie używając kalkulatora, porównaj liczby: 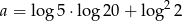2 a = log 5⋅log 20 + log 2 oraz ∘ -----√--- b = 6− 2 5 .

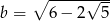Rozwiązanie

Zacznijmy od przekształcenia pierwszej liczby korzystając ze wzoru

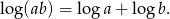
log (ab ) = loga + log b.

Liczymy

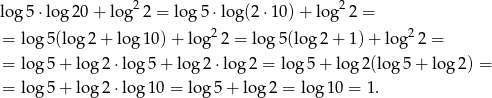
2 2 log 5 ⋅log2 0+ log 2 = log 5⋅ lo g(2⋅ 10)+ lo g 2 = = log 5(log 2+ log 10) + log2 2 = log 5(lo g2 + 1) + log2 2 = = log 5+ lo g2 ⋅log 5+ lo g2 ⋅log 2 = log5 + log 2(log 5+ log 2) = = log 5+ lo g2 ⋅log 10 = log 5+ lo g2 = log 10 = 1.

Jak duża jest druga liczba ustalimy na dwa sposoby.

Sposób I

Nie wiemy, czy liczba 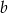jest większa, czy też mniejsza od 1, ale spróbujmy to sprawdzić rozwiązując nierówność

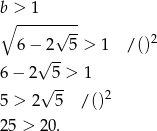
b > 1 ∘ -----√--- 6− 2 5 > 1 / ()2 √ -- 6 − 2 √5-> 1 5 > 2 5 / ()2 25 > 20.

Zatem rzeczywiście 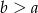b > a .

Sposób II

Tym razem zauważmy, że pod pierwiastkiem mamy pełen kwadrat.

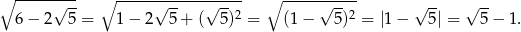
∘ --------- ∘ ------------------ ∘ ----------- √ -- √ -- √ -- √ -- √ -- √ -- 6− 2 5 = 1 − 2 5 + ( 5 )2 = (1 − 5)2 = |1 − 5| = 5 − 1.

Teraz wystarczy zauważyć, że prawdziwa jest nierówność

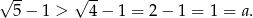
√ -- √ -- 5− 1 > 4− 1 = 2 − 1 = 1 = a.

Odpowiedź: b > a