/Szkoła średnia/Liczby/Logarytmy

Zadanie nr 6963704

Dodaj do ulubionych
Dodaj do rozwiązanych

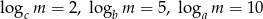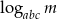Wiedząc, że logc m = 2, logb m = 5, loga m = 10 oblicz logabcm .

Rozwiązanie

Sposób I

Wiemy, że 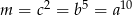m = c2 = b5 = a10 , a musimy ustalić dla jakiego 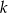k , będzie spełniona równość: 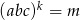k (abc ) = m . Zauważmy, że

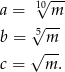
a = 10√m-- √ -- b = 5 m √ -- c = m .

Zatem

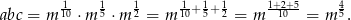
-1 1 1 1+ 1+1 1+2+5- 4 abc = m 10 ⋅ m 5 ⋅m 2 = m 10 5 2 = m 10 = m 5.

To oznacza, że

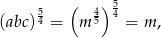
5 ( 4) 5 (abc)4 = m 5 4 = m ,

czyli

5 logabcm = -. 4

Sposób II

Zamieniamy podstawy wszystkich logarytmów na m . Dane równości możemy więc zapisać w postaci:

--1---- 2 = logc m = log c m 5 = log m = --1---- b logm b 1 10 = loga m = ------. logm a

Mamy natomiast obliczyć

log m = ----1-----= -----------1------------ = ----1------= abc logm (abc) logm a + logm b + logm c 110 + 15 + 12 1 1 5 = ------= --= -. 1+210+5- 45 4

 
Odpowiedź: 5 4

Wersja PDF