/Szkoła średnia/Liczby/Logarytmy

Zadanie nr 8852357

Dodaj do ulubionych
Dodaj do rozwiązanych

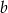Wykaż, że dla każdej dodatniej i różnej od jedności liczby a i dla każdej dodatniej i różnej od jedności liczby b spełniona jest równość

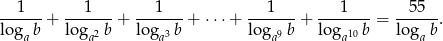
--1---+ --1----+ ---1---+ ⋅⋅⋅+ --1----+ ---1----= --55--. lo gab lo ga2 b loga3 b lo ga9 b loga10 b logab

Rozwiązanie

Na mocy wzoru na zmianę podstawy logarytmu, mamy

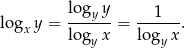
log y log y = ---y--= --1---. x logy x logy x

Mamy zatem

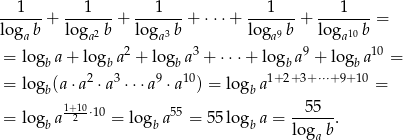
--1--- ---1--- ---1--- ---1--- ---1---- log b + log 2 b + log 3 b + ⋅ ⋅⋅+ log 9 b + log 10 b = a a 2 a 3 a 9 a 10 = logb a + logb a + logb a + ⋅⋅⋅+ logb a + lo gb a = 2 3 9 10 1+2+ 3+ ⋅⋅⋅+9+10 = logb (a⋅a ⋅a ⋅ ⋅⋅a ⋅a ) = logb a = 1+120⋅10 55 --55-- = logb a = logb a = 55logb a = log b. a

Po drodze skorzystaliśmy ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego.

Wersja PDF