Zadanie nr 6835259
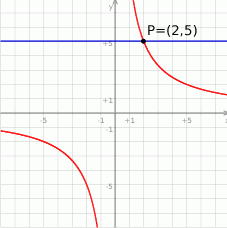
Rysunek przedstawia fragment wykresu funkcji 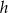 , określonej wzorem
, określonej wzorem 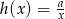 dla
dla 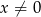 . Wiadomo, że do wykresu funkcji
. Wiadomo, że do wykresu funkcji 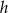 należy punkt
należy punkt 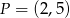 .
.
- Oblicz wartość współczynnika
 .
. - Ustal, czy liczba
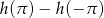 jest dodatnia czy ujemna.
jest dodatnia czy ujemna. - Rozwiąż nierówność
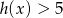 .
.
Rozwiązanie
- Wiemy, że
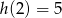 , zatem
, zatem 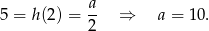
Odpowiedź: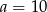
- Z wykresu widzimy, że funkcja
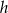 przyjmuje wartości dodatnie dla liczb dodatnich i ujemne dla ujemnych. Zatem
przyjmuje wartości dodatnie dla liczb dodatnich i ujemne dla ujemnych. Zatem 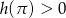 i
i 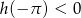 . Stąd
. Stąd 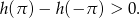
Odpowiedź: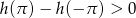
-
Sposób I
Liczymy
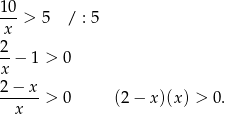
Rozwiązaniem tej nierówności kwadratowej jest przedział
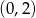 .
. Sposób II
Rozwiązanie podanej nierówności możemy odczytać z wykresu.
Odpowiedź: