Zadanie nr 9337096
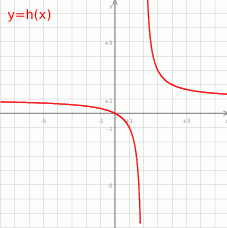
Na rysunku przedstawiono fragment wykresu funkcji 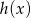 otrzymanego przez przesunięcie o wektor
otrzymanego przez przesunięcie o wektor ![[2,1]](https://img.zadania.info/zad/9337096/HzadT1x.gif) wykresu funkcji
wykresu funkcji 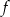 określonej wzorem
określonej wzorem 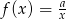 , dla
, dla 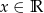 i
i 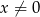 .
.
Wyznacz wzór funkcji 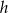 , a następnie sprawdź, czy punkt
, a następnie sprawdź, czy punkt 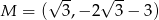 należy do jej wykresu.
należy do jej wykresu.
Rozwiązanie
Korzystamy ze wzoru na przesunięcie funkcji 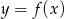 o wektor
o wektor ![→ v = [a,b]](https://img.zadania.info/zad/9337096/HzadR1x.gif) :
:
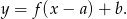
W naszej sytuacji mamy
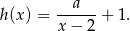
Ponadto z wykresu widać, że 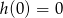 , czyli
, czyli
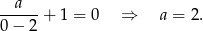
Zatem 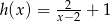 .
.
Liczymy teraz 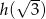 .
.
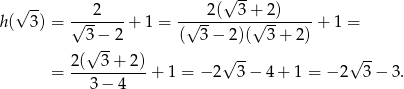
Zatem punkt 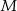 należy do wykresu.
należy do wykresu.
Odpowiedź: 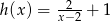 , punkt
, punkt 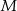 należy do wykresu.
należy do wykresu.

