/Szkoła średnia/Nierówności/Wielomianowe/Z parametrem

Zadanie nr 3117921

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 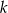k nierówność 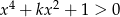4 2 x + kx + 1 > 0 jest prawdziwa dla każdego x ∈ R ?

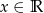Rozwiązanie

Mamy do czynienia z wielomianem dwukwadratowym, podstawmy więc 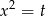x 2 = t .

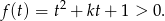
f(t) = t2 + kt+ 1 > 0.

To co musimy ustalić, to kiedy nierówność ta jest spełniona dla wszystkich 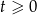t ≥ 0 (bo takie wartości przyjmuje t = x2 ).

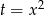Sprawdźmy na początek kiedy ta parabola jest całkowicie powyżej osi 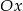Ox .

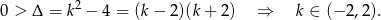
2 0 > Δ = k − 4 = (k − 2)(k + 2) ⇒ k ∈ (− 2,2).

W postałych przypadkach parabola przecina oś 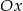Ox i musimy ustalić w jakich punktach (czy na prawo od 0). Zauważmy, że pierwsza współrzędna paraboli to 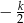− k 2 , zatem dla 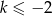k ≤ − 2 parabola ma na pewno dodatnie miejsce zerowe (a miała być powyżej osi dla t ≥ 0 ).

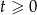Zatem pozostaje przypadek 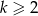k ≥ 2 . Wtedy wierzchołek paraboli jest na lewo od 0 i cała parabola będzie powyżej dodatniej pół-osi 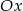Ox jeżeli 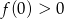f(0) > 0 . Daje to nam nierówność 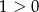1 > 0 , która jest oczywiście zawsze prawdziwa.  
Odpowiedź: k ∈ (− 2,+ ∞ )

Wersja PDF