Zadanie nr 1017060
Wykaż, że równanie 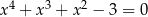 ma tylko jedno rozwiązanie które jest liczbą wymierną.
ma tylko jedno rozwiązanie które jest liczbą wymierną.
Rozwiązanie
Łatwo zauważyć, że jednym z pierwiastków równania jest 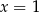 . Dzielimy teraz lewą stronę przez
. Dzielimy teraz lewą stronę przez 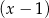 . My jak zwykle zrobimy to grupując wyrazy
. My jak zwykle zrobimy to grupując wyrazy
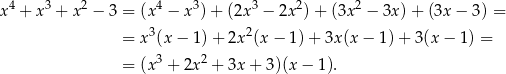
Wystarczy teraz udowodnić, że wielomian w pierwszym nawiasie nie ma pierwiastków wymiernych. W tym celu wystarczy sprawdzić, że żaden z dzielników wyrazu wolnego, czyli 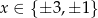 nie jest jego pierwiastkiem. Jest to oczywiste dla
nie jest jego pierwiastkiem. Jest to oczywiste dla 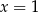 i
i 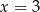 (bo suma na pewno jest dodatnia). Sprawdzamy jeszcze dla
(bo suma na pewno jest dodatnia). Sprawdzamy jeszcze dla 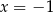 i
i 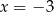 .
.
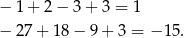
Uwaga. Warto podkreślić, że 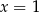 nie jest jedynym rozwiązaniem danego równania – co wyraźnie widać na wykresie jego lewej strony.
nie jest jedynym rozwiązaniem danego równania – co wyraźnie widać na wykresie jego lewej strony.
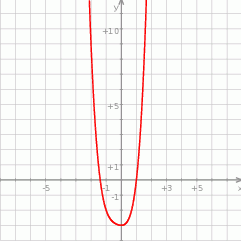
Z naszego rozumowania wynika jednak, że drugi pierwiastek tego równania nie jest liczbą wymierną.

