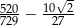Zadanie nr 3206771
Rozważmy równanie 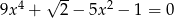 .
.
- Uzasadnij, że równanie to ma 4 pierwiastki.
- Oblicz sumę szóstych potęg wszystkich pierwiastków tego równania.
Rozwiązanie
- Równanie jest dwukwadratowe, więc podstawiamy
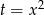 i mamy równanie kwadratowe
i mamy równanie kwadratowe 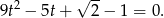
Musimy sprawdzić, że równanie to ma dwa pierwiastki, i że oba są dodatnie. Istotnie, jeżeli
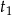 i
i 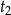 są dodatnimi pierwiastkami tego równania kwadratowego, to pierwiastkami wyjściowego równania są liczby
są dodatnimi pierwiastkami tego równania kwadratowego, to pierwiastkami wyjściowego równania są liczby 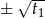 i
i 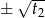 .
. Liczymy
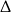 -ę.
-ę. 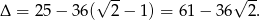
Sprawdźmy czy ta liczba jest dodatnia.
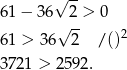
Nierówność jest prawdziwa, więc istotnie
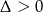 . Pozostało sprawdzić czy oba pierwiastki są dodatnie. Korzystamy ze wzorów Viète’a.
. Pozostało sprawdzić czy oba pierwiastki są dodatnie. Korzystamy ze wzorów Viète’a. 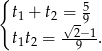
Prawe strony tych równości są dodatnie, więc
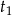 i
i 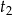 też muszą być dodatnie (z drugiej równości wynika, że obie liczby mają ten sam znak, a z pierwszej, że ten znak to ’+’).
też muszą być dodatnie (z drugiej równości wynika, że obie liczby mają ten sam znak, a z pierwszej, że ten znak to ’+’). - Z poprzedniego podpunktu wiemy, że pierwiastki danego równania to liczby
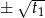 i
i 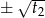 . Zatem suma ich szóstych potęg jest równa
. Zatem suma ich szóstych potęg jest równa 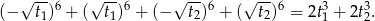
Wyrażenie to obliczymy korzystając z wpisanych w poprzednim podpunkcie wzorów Viète’a, ale najpierw zapiszmy wyrażenie
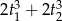 przy pomocy
przy pomocy 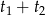 i
i 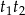 .
. 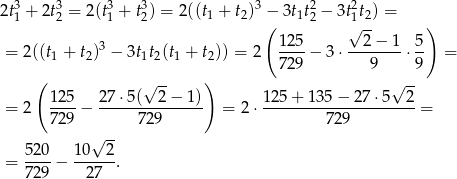
Odpowiedź: