Zadanie nr 7670833
Dany jest wielomian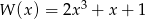 
- Uzasadnij, że wielomian
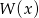nie ma dodatnich pierwiastków. - Uzasadnij, że wielomian
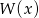nie ma pierwiastków wymiernych. - Uzasadnij, że wielomian
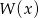ma co najmniej jeden pierwiastek.
Rozwiązanie
- Ponieważ współczynniki wielomianu są dodatnie to
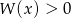dla 
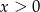. - Pierwiastki wymierne muszą być postaci
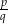, gdzie 
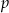dzieli 1, a 
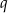dzieli 2. Uwzględniając poprzedni podpunkt, w rachubę wchodzą dwie liczby 
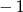i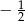 
. Łatwo sprawdzić, że żadana z nich nie jest pierwiastkiem. - Ponieważ wielomian ma stopień 3 i dodatni współczynnik przy najwyższej potędze, jego wykres "zaczyna" się w
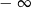i dąży do 
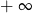(mówiąc odrobinę bardziej precyzyjnie 
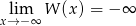i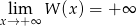 
). Musi więc gdzieś przeciąć oś 
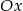(tak naprawdę, tak samo się uzasadnia, że każdy wielomian stopnia 3 ma co najmniej jeden pierwiastek).
