Zadanie nr 3389966
Uzasadnij, że jeżeli współczynniki wielomianu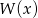 
są liczbami całkowitymi i 
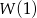jest liczbą nieparzystą, to liczba nieparzysta nie jest pierwiastkiem wielomianu 
.
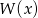Rozwiązanie
W zadaniu chodzi o prostą obserwację, że jeżeli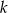 
jest nieparzystą liczbą całkowitą to liczby 
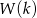i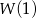 
mają tę samą parzystość. Aby to uzasadnić wystarczy zauważyć, że każdy składnik sumy
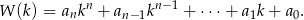
ma taką samą parzystość jak odpowiadający składnik sumy
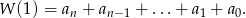
Mówiąc jeszcze dokładniej, jeżeli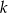 
jest nieparzyste, to o tym czy 
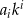jest parzyste czy nie, decyduje parzystość 
.
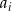Zatem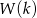 
, tak jak 
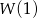, jest liczbą nieparzystą, nie może więc być równe 0.
