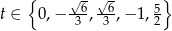/Szkoła średnia/Równania/Wielomianowe/Różne

Zadanie nr 4616099

Rozwiąż równanie 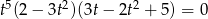5 2 2 t (2− 3t )(3t − 2t + 5) = 0 .

Wersja PDF

Rozwiązanie

Jednym z pierwiastków równania jest oczywiście 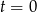t = 0 . Pozostałe pierwiastki wyznaczamy sprawdzając, kiedy zerują się wyrażenia w nawiasach.

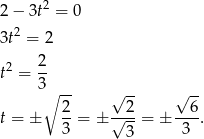
2 2 − 3t = 0 3t2 = 2 t2 = 2- 3 ∘ -2 √ 2- √ 6- t = ± --= ± √---= ± ---. 3 3 3

Pozostało rozwiązać równanie kwadratowe

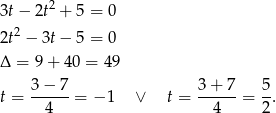
2 3t− 2t + 5 = 0 2t2 − 3t− 5 = 0 Δ = 9+ 40 = 49 3 − 7 3 + 7 5 t = ------= − 1 ∨ t = ------= -. 4 4 2

Równanie ma więc 5 rozwiązań

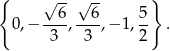
{ } √ 6- √ 6- 5 0,− ----,---,− 1, -- . 3 3 2

 
Odpowiedź: { √- √- } t ∈ 0,− -6, -6,− 1, 5 3 3 2

Wersja PDF