/Szkoła średnia/Równania/Wielomianowe/Różne

Zadanie nr 6390705

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że równanie 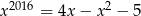2016 2 x = 4x − x − 5 nie ma rozwiązań rzeczywistych.

Rozwiązanie

Sposób I

Aby wykazać, że dane równanie jest sprzeczne wystarczy zauważyć, że lewa strona tego równania jest zawsze nieujemna, natomiast prawa strona

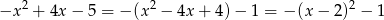
−x 2 + 4x− 5 = − (x2 − 4x + 4) − 1 = − (x − 2)2 − 1

jest zawsze ujemna.

Sposób II

Ujemność prawej strony równania możemy też uzasadnić badając funkcję kwadratową

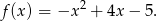
f(x ) = −x 2 + 4x − 5.

Jej wykresem jest parabola o ramionach skierowanych w dół i pierwszej współrzędnej wierzchołka równej

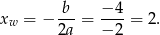
b − 4 xw = − 2a-= −-2-= 2.

Największą wartością tej funkcji jest więc

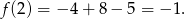
f (2) = − 4+ 8− 5 = − 1.

Na koniec wykres funkcji f .

PIC
Wersja PDF