/Konkursy/Zadania/Równania/Wielomianowe/Różne

Zadanie nr 1779573

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian 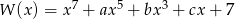7 5 3 W (x) = x + ax + bx + cx+ 7 jest podzielny przez wielomian 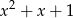x 2 + x + 1 . Wyznacz resztę z dzielenia wielomianu 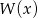W (x ) przez wielomian x 2 − x + 1 .

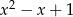Rozwiązanie

Wiemy, że 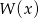W (x ) dzieli się przez 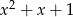2 x + x + 1 , więc

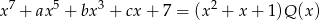
7 5 3 2 x + ax + bx + cx + 7 = (x + x+ 1)Q (x)

dla pewnego wielomianu 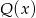Q (x) . Podstawmy w tej równości 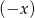(−x ) zamiast x .

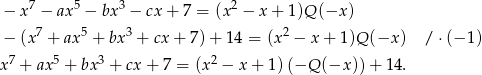
7 5 3 2 − x − ax − bx − cx + 7 = (x − x + 1 )Q(−x ) 7 5 3 2 − (x + ax + bx + cx + 7) + 14 = (x − x + 1 )Q(−x ) / ⋅(− 1) x7 + ax5 + bx3 + cx + 7 = (x2 − x+ 1)(−Q (−x ))+ 14.

Widać teraz, że wielomian 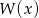W (x ) przy dzieleniu przez wielomian 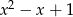2 x − x + 1 daje resztę 14.  
Odpowiedź: 14

Wersja PDF