Zadanie nr 3337037
Wielomian 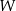 jest wielomianem stopnia 5 i spełnia warunki:
jest wielomianem stopnia 5 i spełnia warunki: 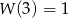 oraz
oraz 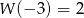 . Wykaż, że nie wszystkie współczynniki wielomianu
. Wykaż, że nie wszystkie współczynniki wielomianu 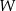 są liczbami całkowitymi.
są liczbami całkowitymi.
Rozwiązanie
Sposób I
Przypuśćmy, że współczynniki wielomianu 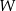 są liczbami całkowitymi i niech
są liczbami całkowitymi i niech
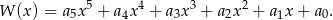
Zapisując warunki 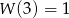 i
i 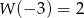 otrzymujemy
otrzymujemy
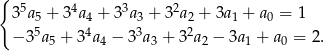
Jeżeli dodamy te równości stronami otrzymamy
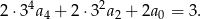
Zauważmy teraz, że każda z liczb 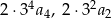 jest podzielna przez 3; podzielna przez 3 jest też prawa strona. To oznacza, że
jest podzielna przez 3; podzielna przez 3 jest też prawa strona. To oznacza, że 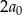 musi być liczbą podzielną przez 3, czyli przez 3 musi dzielić się
musi być liczbą podzielną przez 3, czyli przez 3 musi dzielić się 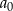 . To jednak jest sprzeczność z równością
. To jednak jest sprzeczność z równością
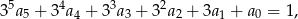
bo w takiej sytuacji lewa strona dzieli się przez 3, a prawa nie.
Sposób II
Dokładnie tak samo jak w poprzednim sposobie dochodzimy do równości
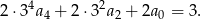
Zauważmy teraz, że lewa strona jest parzysta, a prawa nie. Sprzeczność.
Sposób III
Zadanie robi się banalne, jeżeli znamy następujący fakt:
Jeżeli 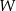 jest wielomianem o współczynnikach całkowitych, to dla dowolnych liczb całkowitych
jest wielomianem o współczynnikach całkowitych, to dla dowolnych liczb całkowitych 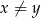 liczba
liczba 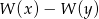 dzieli się przez
dzieli się przez 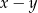 .
.
Fakt ten łatwo uzasadnić posługując się wzorem skróconego mnożenia na 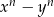 .
.
W naszej sytuacji mamy 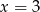 i
i 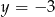 , czyli gdyby wielomian
, czyli gdyby wielomian 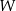 miał współczynniki całkowite, to mielibyśmy podzielność liczby
miał współczynniki całkowite, to mielibyśmy podzielność liczby
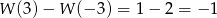
przez
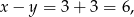
co stanowi sprzeczność.

