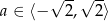/Szkoła średnia/Równania/Trygonometryczne/Z parametrem

Zadanie nr 2873052

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbadaj dla jakich wartości parametru a istnieje rozwiązanie równania

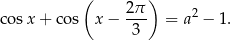
( 2 π) cos x+ cos x − --- = a2 − 1. 3

Rozwiązanie

Korzystamy ze wzoru

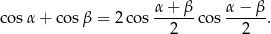
α+ β α − β co sα + cos β = 2 cos ------cos------. 2 2

na sumę cosinusów.

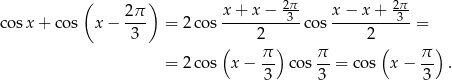
( 2π ) x + x− 2π- x− x+ 2π- cosx + co s x − --- = 2 cos---------3- cos ---------3-= 3 ( 2 ) 2 ( ) π- π- π- = 2 cos x− 3 cos 3 = cos x− 3 .

Interesuje nas więc równanie

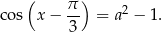
( ) π- 2 cos x − 3 = a − 1 .

Równanie to ma rozwiązania wtedy i tylko wtedy, gdy

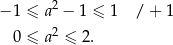
− 1 ≤ a2 − 1 ≤ 1 / + 1 2 0 ≤ a ≤ 2.

Lewa nierówność jest zawsze spełniona, a rozwiązaniem prawej jest przedział 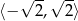√ --√ -- ⟨− 2, 2⟩ .  
Odpowiedź: √ --√ -- a ∈ ⟨− 2, 2⟩

Wersja PDF