/Szkoła średnia/Równania/Trygonometryczne/Z parametrem

Zadanie nr 5774728

Wyznacz wszystkie wartości parametru 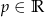p ∈ R , dla których równanie 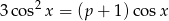3 cos2x = (p + 1)co sx ma w przedziale 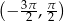( ) − 3π2 , π2 tylko trzy różne rozwiązania, z których dwa są ujemne, a jedno dodatnie.

Wersja PDF

Rozwiązanie

Zauważmy, że równanie będzie spełnione jeżeli 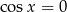cosx = 0 . W danym przedziale daje to od razu jedno rozwiązanie: x = − π2 .

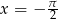Jeżeli 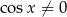cos x ⁄= 0 to możemy równanie podzielić przez 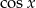cosx i zostaje

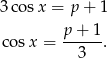
3cos x = p + 1 p + 1 cos x = ------. 3

Pytanie zatem brzmi: dla jakich wartości 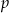p powyższe równanie ma dokładnie dwa rozwiązania, które ponadto różnią się znakiem? Szkicujemy funkcję cosinus.

PIC

Z wykresu widać, że w przedziale 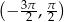( ) − 3π2-, π2 równanie 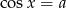cosx = a ma dwa rozwiązania różnych znaków wtedy i tylko wtedy, gdy 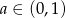a ∈ (0,1 ) . Mamy zatem

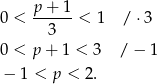
p+--1- 0 < 3 < 1 / ⋅3 0 < p + 1 < 3 / − 1 − 1 < p < 2.

 
Odpowiedź: p ∈ (− 1,2 )

Wersja PDF