Zadanie nr 6504779
Wyznacz zbiór wartości parametru 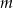 , dla których równanie:
, dla których równanie: 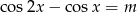 ma rozwiązania.
ma rozwiązania.
Rozwiązanie
Musimy wyznaczyć zbiór wartości funkcji
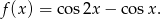
Równanie będzie miało rozwiązanie dokładnie wtedy, gdy 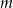 będzie elementem zbioru wartości tej funkcji.
będzie elementem zbioru wartości tej funkcji.
Na mocy wzoru na 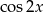 mamy
mamy
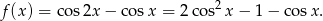
Jeżeli podstawimy teraz 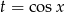 to mamy funkcję kwadratową
to mamy funkcję kwadratową
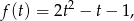
określoną na przedziale 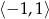 (takie wartości przyjmuje
(takie wartości przyjmuje 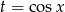 ). Zauważmy, że ramiona paraboli będącej wykresem tej funkcji są skierowane w górę, a jej wierzchołek ma współrzędne
). Zauważmy, że ramiona paraboli będącej wykresem tej funkcji są skierowane w górę, a jej wierzchołek ma współrzędne
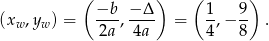
Pierwsza współrzędna wierzchołka znajduje się w przedziale 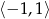 , więc najmniejsza wartość funkcji będzie równa
, więc najmniejsza wartość funkcji będzie równa 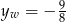 . Największą wartość otrzymamy w jednym z końców przedziału
. Największą wartość otrzymamy w jednym z końców przedziału 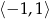 , w którym? – liczymy i sprawdzamy.
, w którym? – liczymy i sprawdzamy.
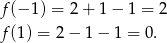
Zatem zbiorem wartości funkcji 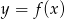 jest przedział
jest przedział 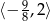 i dokładnie dla takich wartości parametru
i dokładnie dla takich wartości parametru 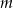 dane równanie ma rozwiązania.
dane równanie ma rozwiązania.
Na koniec wykresy funkcji 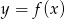 i
i  .
.
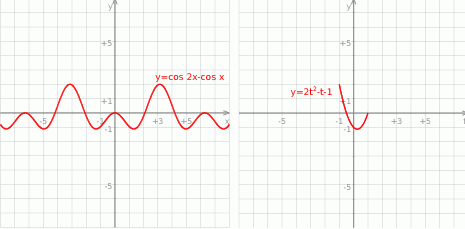
Odpowiedź: