/Konkursy/Zadania/Równania/W liczbach całkowitych

Zadanie nr 2521932

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie liczby naturalne dodatnie 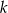k , dla których równanie 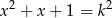x 2 + x + 1 = k2 ma pierwiastki będące liczbami całkowitymi.

Rozwiązanie

Dane równanie

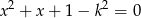
2 2 x + x + 1 − k = 0

to równanie kwadratowe, obliczmy jego wyróżnik.

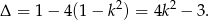
2 2 Δ = 1 − 4(1 − k ) = 4k − 3.

Ponieważ współczynniki w powyższym równaniu są całkowite, pierwiastki równania

√ -- −b--±---Δ- 2

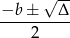
mogą być liczbami całkowitymi tylko wtedy, gdy 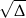√ -- Δ jest liczbą całkowitą, czyli wtedy, gdy 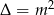Δ = m 2 dla pewnej liczby całkowitej 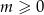m ≥ 0 . Mamy więc warunek

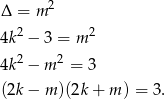
Δ = m 2 4k2 − 3 = m 2 2 2 4k − m = 3 (2k− m )(2k + m) = 3.

Ponieważ z założenia liczby 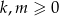k,m ≥ 0 są całkowite, jedynym możliwym rozwiązaniem powyższej równości jest

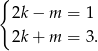
{ 2k − m = 1 2k + m = 3.

Dodając równania stronami mamy 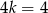4k = 4 , czyli 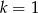k = 1 . Równanie przybiera wtedy postać

x2 + x = 0

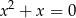
i oczywiście jego pierwiastki są liczbami całkowitymi.  
Odpowiedź: k = 1

Wersja PDF