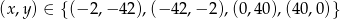Zadanie nr 3202710
Wyznacz wszystkie liczby całkowite 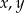 spełniające równanie
spełniające równanie 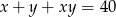 .
.
Rozwiązanie
Przekształćmy dane równanie.
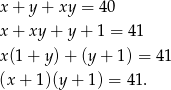
Liczba 41 jest liczbą pierwszą więc możliwe są 4 przypadki
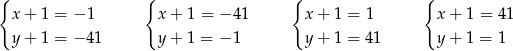
Otrzymujemy stąd 4 rozwiązania
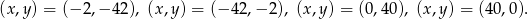
Odpowiedź: 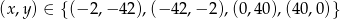
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz wszystkie liczby całkowite 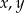 spełniające równanie
spełniające równanie 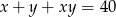 .
.
Przekształćmy dane równanie.
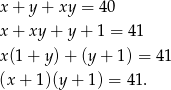
Liczba 41 jest liczbą pierwszą więc możliwe są 4 przypadki
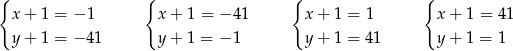
Otrzymujemy stąd 4 rozwiązania
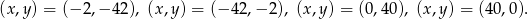
Odpowiedź: