Zadanie nr 6983037
Wykaż, że jeżeli liczby całkowite 
i 
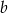spełniają równanie
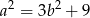
to liczba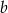 
dzieli się przez 3, a liczba 
nie dzieli się przez 9.
Rozwiązanie
Zauważmy, że prawa strona danej równości dzieli się przez 3, zatem 
też musi dzielić się przez 3. Zatem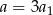 
dla pewnej liczby całkowitej 
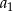. Podstawiając to wyrażenie w danej równości otrzymujemy
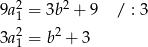
Teraz widać, że liczba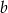 
też musi dzielić się przez 3. Zatem 
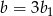dla pewnego 
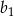. Podstawiamy to wyrażenie.
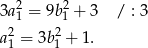
Zauważmy teraz, że gdyby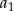 
dzieliło się przez 3, to otrzymalibyśmy, że 1 dzieli się przez 3, co nie jest możliwe. Zatem 
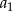nie dzieli się przez 3, czyli 
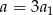nie dzieli się przez 9.
