Zadanie nr 8366833
Iloczyn trzech liczb pierwszych jest pięć razy większy od ich sumy. Wyznacz te liczby.
Rozwiązanie
Musimy znaleźć liczby pierwsze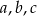 
spełniające równanie
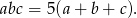
Zauważmy, że prawa strona dzieli się przez 5, więc lewa strona też musi dzielić się przez 5. To oznacza, że jedna z szukanych liczb musi być równa 5. Powiedzmy, że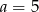 
. Mamy więc równanie
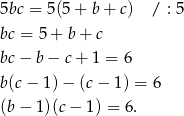
Aby zmniejszyć liczbę możliwości załóżmy, że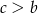 
. Mamy zatem dwie możliwości
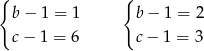
W drugim przypadku mamy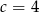 
, co jest sprzeczne z tym, że szukamy liczb pierwszych. Zatem musi zachodzić pierwszy przypadek, czyli dwie pozostałe liczby to 2 i 7.
Odpowiedź: 2,5,7
