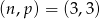Zadanie nr 9147597
Wyznacz wszystkie liczby pierwsze  i liczby naturalne
i liczby naturalne  spełniające równość
spełniające równość
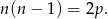
Rozwiązanie
Z danej równości wynika, że  jest dzielnikiem liczby
jest dzielnikiem liczby 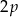 . Zatem
. Zatem 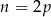 lub
lub 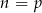 lub
lub 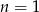 . Sprawdźmy po kolei te przypadki.
. Sprawdźmy po kolei te przypadki.
Jeżeli 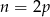 to
to 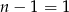 , czyli
, czyli 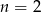 . Wtedy jednak
. Wtedy jednak 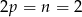 , co nie jest możliwe.
, co nie jest możliwe.
Jeżeli 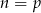 to
to 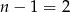 , czyli
, czyli 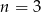 i mamy rozwiązanie
i mamy rozwiązanie  .
.
Jeżeli natomiast 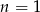 to
to 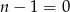 , co nie jest możliwe.
, co nie jest możliwe.
Odpowiedź: