/Szkoła średnia/Prawdopodobieństwo/Schemat Bernoullego

Zadanie nr 2134480

Dodaj do ulubionych
Dodaj do rozwiązanych

Prawdopodobieństwo wystąpienia awarii oświetlenia ulic w pewnym mieście w godzinach wieczornych pojedynczego dnia jest równe 0,2. Oblicz prawdopodobieństwo zdarzenia 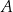A polegającego na tym, że w okresie sześciu dni wystąpią co najwyżej trzy takie dni, w których nastąpi awaria oświetlenia ulic w tym mieście w godzinach wieczornych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.

Rozwiązanie

Zadanie możemy rozwiązać przy pomocy schematu Bernoulliego. Jeżeli przez sukces rozumiemy wystąpienie awarii, to interesuje nas prawdopodobieństwo otrzymania co najwyżej trzech sukcesów w sześciu próbach.

( ) ( ) ( ) ( ) 6 0 6 6 5 6 2 4 6 3 3 P(A ) = 0 p (1 − p) + 1 p(1 − p) + 2 p (1 − p) + 3 p (1− p) = ( ) = (1 − p )3 (1− p)3 + 6p(1 − p)2 + 6-⋅5 ⋅p2(1 − p) + 6-⋅5-⋅4 ⋅p3 = 2 3! 3( 3 2 2 3) = (1 − p ) (1 − p ) + 6p (1− p) + 15p (1 − p) + 20p = ( ) = 0,8 3 ⋅ 0,83 + 6 ⋅0,2 ⋅0,82 + 15 ⋅0,22 ⋅0,8+ 20 ⋅0,23 = = 0,5 12⋅(0 ,5 12+ 0,768 + 0,48 + 0,16 ) = 0,512 ⋅1,92 = 0 ,98304 ≈ 0 ,�

 
Odpowiedź: 0,98

Wersja PDF