/Szkoła średnia/Prawdopodobieństwo/Schemat Bernoullego

Zadanie nr 4935078

Z trzech urn, w których jest po 2 kule białe i 3 czarne, wyjmujemy po jednej kuli i wkładamy do czwartej urny, w której była jedna kula biała. Losujemy teraz jedną kulę z czwartej urny. Oblicz prawdopodobieństwo, że z czwartej urny wyjmiemy białą kulę.

Wersja PDF

Rozwiązanie

Sposób I

Do czwartej urny dokładamy trzy kule. Prawdopodobieństwo wylosowania białej kuli z tej urny zależy więc od tego, ile białych kul dokładamy. Mamy cztery możliwości
B: dokładamy same białe kule,
C: dokładamy dwie kule białe,
D: dokładamy jedną kulę białą,
E: dokładamy same czarne kule.
Prawdopodobieństwa tych zdarzeń najprościej obliczyć ze schematu Bernoulliego. Za sukces uważamy wylosowanie białej kuli, mamy zatem 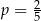2 p = 5 . Stąd

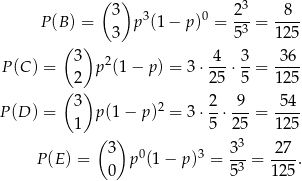
( ) 3 P(B ) = 3 p3(1− p)0 = 2--= -8-- 3 5 3 125 (3 ) 4 3 36 P (C ) = p 2(1− p) = 3 ⋅---⋅--= ---- (2 ) 25 5 125 3 2 2- -9- -54- P (D ) = 1 p (1− p) = 3 ⋅5 ⋅25 = 125 ( ) 3 0 3 33- 27-- P (E) = 0 p (1 − p) = 53 = 125.

Możemy teraz narysować drzewko, którego pierwszy wiersz to zdarzenia 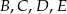B ,C,D ,E , a w drugim wierszu mamy zdarzenia wylosowania odpowiedniej kuli z czwartej urny. Interesujące nas zdarzenie 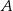A , czyli wylosowanie białej kuli, oznaczyliśmy na czerwono.

PIC

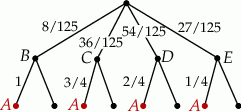
Z drzewka odczytujemy

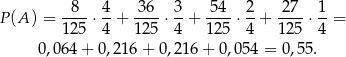
8 4 36 3 54 2 27 1 P (A) = ----⋅--+ ----⋅--+ ----⋅--+ ---- ⋅--= 125 4 125 4 125 4 1 25 4 0 ,0 64+ 0,216 + 0,216 + 0,0 54 = 0,55.

Sposób II

Tym razem pomyślmy sobie inaczej. Losując z czwartej urny, wybieramy spośród 4 kul. Jedna z nich jest biała i wybieramy ją z prawdopodobieństwem 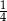14 (bo w urnie są 4 kule). Ponadto z prawdopodobieństwem 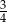3 4 wybieramy jedną kulę z trzech przełożonych z innych urn. Zatem interesujące nas prawdopodobieństwo wynosi

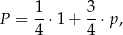
1 3 P = --⋅1 + -⋅ p, 4 4

gdzie 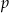p jest prawdopodobieństwem wybrania białej kuli spośród trzech kul wybranych z pierwszych trzech urn. To prawdopodobieństwo jest po prostu równe prawdopodobieństwu wybrania białej kuli z trzech pierwszych urn, czyli jest równe 2 5 . Mamy więc

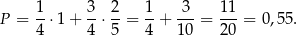
1- 3- 2- 1- 3-- 11- P = 4 ⋅1 + 4 ⋅ 5 = 4 + 10 = 20 = 0,55.

 
Odpowiedź: 0,55

Wersja PDF