/Szkoła średnia/Prawdopodobieństwo/Schemat Bernoullego

Zadanie nr 6088715

Dodaj do ulubionych
Dodaj do rozwiązanych

Rzucamy 7 razy dwiema monetami. Oblicz prawdopodobieństwo, że co najmniej 6 razy wyrzucimy dwie reszki.

Rozwiązanie

Sposób I

Zadanie możemy rozwiązać przy pomocy schematu Bernoulliego. Pojedyncza próba to rzut dwoma monetami. Prawdopodobieństwo sukcesu w takiej próbie (czyli prawdopodobieństwo wyrzucenia 2 reszek) wynosi

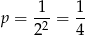
p = 1--= 1- 22 4

(bo sprzyjające zdarzenie to (R,R)).

Zatem prawdopodobieństwo uzyskania co najmniej 6 sukcesów w 7 próbach to

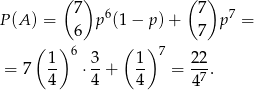
( ) ( ) 7 6 7 7 P(A ) = 6 p (1− p) + 7 p = ( ) ( ) 1- 6 3- 1- 7 22- = 7 4 ⋅4 + 4 = 47.

Sposób II

Możemy też obyć się bez schematu Bernoulliego. Za zdarzenia elementarne przyjmujemy 7 elementowe ciągi otrzymanych par wyrzuconych monet. Mamy 4 możliwe pary, więc

|Ω | = 47.

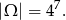
Interesujące nas wyniki to takie, że są same reszki – takie zdarzenie jest jedno; lub, że są same reszki z wyjątkiem jednej pary, gdzie nie ma dwóch reszek. Miejsce dla tej wyróżnionej pary możemy wybrać na 7 sposobów, a samą parę na 3 sposoby (wszystko oprócz dwóch reszek). Zatem prawdopodobieństwo wynosi

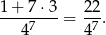
1+--7⋅3- 22- 47 = 4 7.

 
Odpowiedź: 227 4

Wersja PDF