/Szkoła średnia/Prawdopodobieństwo/Schemat Bernoullego

Zadanie nr 9224302

Dodaj do ulubionych
Dodaj do rozwiązanych

Kasia i Ula grają w warcaby i każda rozgrywka kończy się wygraną jednej z dziewczynek. Prawdopodobieństwo wygrania pojedynczej partii przez Ulę jest równe 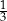13 . Oblicz prawdopodobieństwo wygrania przez Kasię co najmniej sześciu z siedmiu rozegranych partii. Wynik podaj w postaci ułamka zwykłego nieskracalnego.

Rozwiązanie

Zadanie możemy rozwiązać przy pomocy schematu Bernoulliego. Pojedyncza próba to jedna partia warcabów. Prawdopodobieństwo sukcesu w takiej próbie (czyli prawdopodobieństwo wygranej Kasi) wynosi 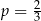p = 23 . Zatem prawdopodobieństwo uzyskania co najmniej 6 sukcesów w 7 próbach to

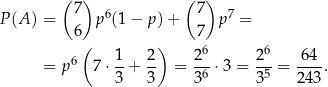
( 7) (7 ) P (A ) = p 6(1− p)+ p 7 = 6 7 ( 1 2) 26 26 64 = p6 7 ⋅--+ -- = -6-⋅3 = -5-= ----. 3 3 3 3 24 3

 
Odpowiedź: 26443

Wersja PDF