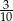Zadanie nr 9272780
Rzucono dziesięć razy kostką do gry. Oblicz prawdopodobieństwo, że już w pierwszym rzucie wypadła szóstka, jeśli w ogóle wypadły trzy szóstki.
Rozwiązanie
Sposób I
To co mamy policzyć to prawdopodobieństwo warunkowe
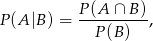
gdzie 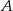 jest zdarzeniem polegającym na wyrzuceniu 6 za pierwszym razem, a
jest zdarzeniem polegającym na wyrzuceniu 6 za pierwszym razem, a 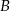 zdarzeniem polegającym na wyrzuceniu 3 szóstek w 10 rzutach.
zdarzeniem polegającym na wyrzuceniu 3 szóstek w 10 rzutach.
Możemy myśleć, że mamy schemat Bernoulliego, gdzie za sukces przyjmujemy wyrzucenie szóstki (czyli prawdopodobieństwo sukcesu jest równe 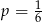 ). Prawdopodobieństwo otrzymania 3 sukcesów w 10 próbach jest równe
). Prawdopodobieństwo otrzymania 3 sukcesów w 10 próbach jest równe
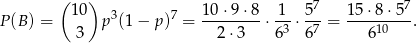
Obliczymy teraz 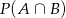 , czyli prawdopodobieństwo 3 szóstek w 10 rzutach, przy czym jedna z nich jest na pierwszym miejscu. Szóstka na pierwszym miejscu pojawia się z prawdopodobieństwem
, czyli prawdopodobieństwo 3 szóstek w 10 rzutach, przy czym jedna z nich jest na pierwszym miejscu. Szóstka na pierwszym miejscu pojawia się z prawdopodobieństwem 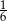 , a prawdopodobieństwo otrzymania 2 szóstek w pozostałych 9 rzutach liczymy ze schematu Bernoulliego.
, a prawdopodobieństwo otrzymania 2 szóstek w pozostałych 9 rzutach liczymy ze schematu Bernoulliego.
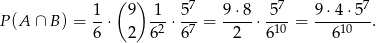
Zatem szukane prawdopodobieństwo wynosi
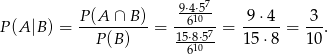
Sposób II
Przyjmijmy za zdarzenia elementarne ciągi otrzymanych liczb oczek, przy czym od razu zakładamy, że wśród otrzymanych wyników są dokładnie 3 szóstki. Obliczmy ile jest takich ciągów: pozycje 6-tek możemy wybrać na
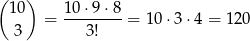
sposobów, a na pozostałych 7 miejscach wyniki są dowolne, ale różne od 6. Zatem
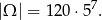
W zdarzeniach sprzyjających na pierwszym miejscu jest 6. Miejsca pozostałych dwóch 6-tek możemy wybrać na
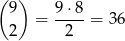
sposobów, a na pozostałych 7 miejscach wyniki są dowolne, ale różne od 6. Jest więc
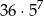
zdarzeń sprzyjających i prawdopodobieństwo
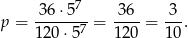
Odpowiedź: