/Szkoła średnia/Prawdopodobieństwo/Schemat Bernoullego

Zadanie nr 9648201

Ile razy trzeba rzucać trzema monetami, aby prawdopodobieństwo otrzymania co najmniej raz jednocześnie trzech orłów było większe od 0,8?

Wersja PDF

Rozwiązanie

Najprościej jest myśleć, że mamy schemat Bernoulliego, gdzie pojedyncza próba polega na jednoczesnym rzucie trzema monetami. Prawdopodobieństwo wyrzucenia jednocześnie trzech orłów (sukcesu) jest równe

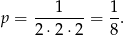
p = ---1--- = 1-. 2 ⋅2 ⋅2 8

Ponieważ interesuje na prawdopodobieństwo co najmniej jednego sukcesu, to łatwiej jest zajmować się prawdopodobieństwem samych porażek. Musimy ustalić kiedy jest nie większe niż 0,2. Na mocy wzoru Bernoulliego mamy

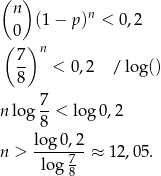
(n ) (1− p)n < 0,2 ( 0 ) 7- n 8 < 0,2 / log() n log 7-< log0 ,2 8 lo g0,2 n > ----7--≈ 12,05. log 8

 
Odpowiedź: Co najmniej 13 razy.

Wersja PDF