Zadanie nr 9984789
Dwaj równorzędni przeciwnicy grają w szachy. Co jest bardziej prawdopodobne:
- wygranie dwóch partii z trzech, czy czterech partii z sześciu rozegranych?
- wygranie nie mniej niż dwóch partii z trzech, czy nie mniej niż czterech partii z sześciu rozegranych? (Remisów nie uwzględniamy.)
Rozwiązanie
Aby zadanie było prostsze, lepiej sobie myśleć, że rzucamy symetryczną monetą, jeżeli wypada reszka to wygrywa pierwszy, jeżeli orzeł to drugi. W szczególności widać, że zadanie można rozwiązać zwykłym schematem Bernoulliego.
Za zdarzenia elementarne przyjmujemy uporządkowany ciąg wyników kolejnych rzutów (partii). Zatem
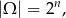
gdzie  –ilość prób. Umówmy się ponadto, że reszka to sukces.
–ilość prób. Umówmy się ponadto, że reszka to sukces.
- Szukane prawdopodobnieństwa wynoszą odpowiednio (schemat Bernoulliego)
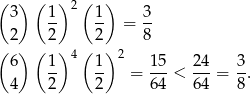
Odpowiedź: Dwóch partii z trzech - Jak wyżej, prawdopodobieństwa wynoszą odpowiednio
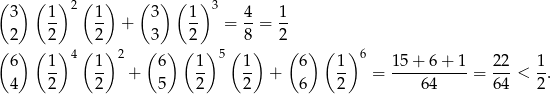
Odpowiedź: Nie mniej niż dwóch partii z trzech

