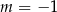Zadanie nr 1946283
Wyznacz wszystkie wartości parametru 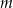 , dla których suma odwrotności pierwiastków równania
, dla których suma odwrotności pierwiastków równania
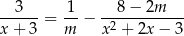
jest równa 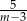 .
.
Rozwiązanie
Oczywiście musi być 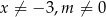 i
i 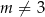 . Sprawdźmy jeszcze kiedy zeruje się trójmian w mianowniku.
. Sprawdźmy jeszcze kiedy zeruje się trójmian w mianowniku.
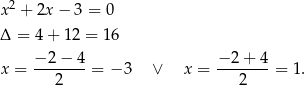
Musimy więc dodatkowo założyć, że 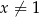 . Przy okazji okazało się również, że
. Przy okazji okazało się również, że
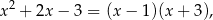
co pozwala dość łatwo pozbyć się ułamków w równaniu.
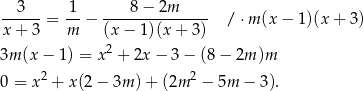
Otrzymaliśmy więc zwykłe równanie kwadratowe z parametrem. Sprawdźmy, kiedy równanie to ma pierwiastki.
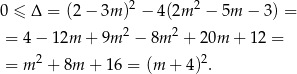
Równanie ma więc zawsze pierwiastki i możemy skorzystać ze wzorów Viète’a.
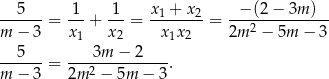
Zanim rozwiążemy to równanie, bądźmy ostrożni i sprawdźmy, jakie są miejsca zerowe mianownika.
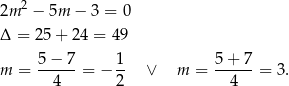
Zakładamy więc dodatkowo, że 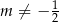 . Przy okazji okazało się, że
. Przy okazji okazało się, że
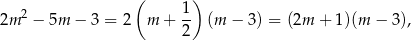
co pozwala łatwo uprościć równanie
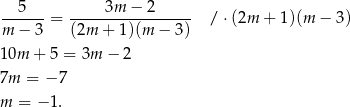
Na koniec sprawdźmy, czy otrzymana wartość 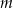 spełnia wszystkie poczynione wcześniej założenia. Wprawdzie nigdzie nie założyliśmy, że
spełnia wszystkie poczynione wcześniej założenia. Wprawdzie nigdzie nie założyliśmy, że 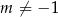 , ale założyliśmy, że
, ale założyliśmy, że 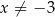 i
i 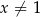 . Sprawdźmy więc, czy rozwiązaniem równania dla
. Sprawdźmy więc, czy rozwiązaniem równania dla 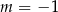 nie jest jedna z tych liczb. Równanie kwadratowe dla
nie jest jedna z tych liczb. Równanie kwadratowe dla 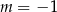 przyjmuje postać
przyjmuje postać
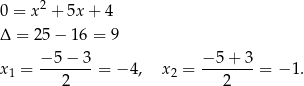
Zatem wszystko jest w porządku (widać też, że rzeczywiście 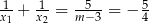 ).
).
Odpowiedź: