/Szkoła średnia/Równania/Wymierne/Z parametrem

Zadanie nr 2622683

Dodaj do ulubionych
Dodaj do rozwiązanych

Określ liczbę rozwiązań równania 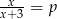-x-- x+3 = p w zależności od wartości parametru p .

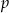Rozwiązanie

Sposób I

Przekształcamy podane równanie (mnożymy przez mianownik).

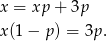
x = xp + 3p x(1− p) = 3p .

Możliwe są różne sytuacje. Jeżeli 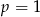p = 1 , to mamy sprzeczną równość 0 = 3 .

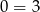Jeżeli 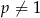p ⁄= 1 , to z powyższego równania mamy

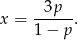
3p x = ------. 1 − p

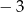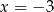Mogłoby się wydawać, że oznacza to, że równanie ma jedno rozwiązanie, ale jest małe ’ale’. Musimy mianowicie sprawdzić, czy to rozwiązanie nie jest przypadkiem równe − 3 , dla x = − 3 mianownik w wyjściowym równaniu się zeruje. Sprawdźmy kiedy tak jest.

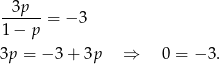
--3p-- 1 − p = − 3 3p = −3 + 3p ⇒ 0 = − 3.

Zatem taka sytuacja nigdy nie zachodzi.

Sposób II

Z lewej strony danego równania mamy funkcję homograficzną

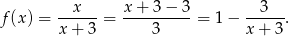
f (x) = --x---= x-+-3-−-3-= 1− --3--. x + 3 3 x+ 3

Wykres tej funkcji jest hiperbolą 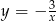y = − 3x przesuniętą o 3 jednostki w lewo i 1 jedną jednostkę do góry.

PIC

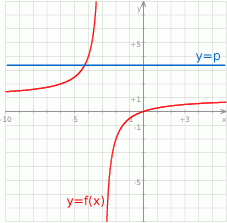
Jeżeli naszkicujemy ten wykres, to widać, że dane równanie ma jedno rozwiązanie dla 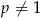p ⁄= 1 i jest sprzeczne dla p = 1 .  
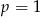Odpowiedź: Jedno rozwiązanie dla 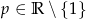p ∈ R ∖{ 1} , brak rozwiązań dla p = 1

Wersja PDF