Zadanie nr 9304850
Wykaż, że dla dowolnych liczb rzeczywistych 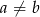 oraz
oraz 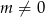 równanie
równanie
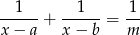
ma dwa różne rozwiązania.
Rozwiązanie
Przekształcamy dane równanie
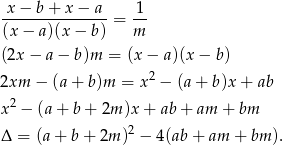
Wyrażenie 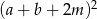 możemy obliczyć wymnażając dwa nawiasy, ale możemy też skorzystać ze wzoru
możemy obliczyć wymnażając dwa nawiasy, ale możemy też skorzystać ze wzoru
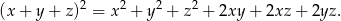
Mamy więc
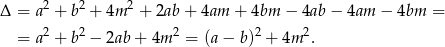
Ponieważ z założenia 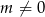 , więc
, więc 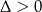 , co oznacza, że równanie ma zawsze dwa pierwiastki. Nie jest to jednak całkiem koniec, bo musimy sprawdzić, czy jeden z tych pierwiastków to nie jest przypadkiem
, co oznacza, że równanie ma zawsze dwa pierwiastki. Nie jest to jednak całkiem koniec, bo musimy sprawdzić, czy jeden z tych pierwiastków to nie jest przypadkiem  lub
lub 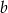 (liczby te nie należą do dziedziny równania). Sprawdzamy podstawiając
(liczby te nie należą do dziedziny równania). Sprawdzamy podstawiając  i
i 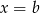 w otrzymanym równaniu kwadratowym.
w otrzymanym równaniu kwadratowym.
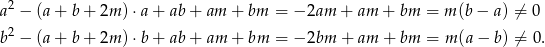
Zatem rzeczywiście pierwiastkiem nie może być ani liczba  , ani
, ani 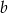 .
.

