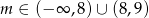/Szkoła średnia/Równania/Wymierne/Z parametrem

Zadanie nr 9641771

Wyznacz te wartości parametru m , dla których równanie 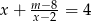m−8- x + x−2 = 4 ma

  • dokładnie jedno rozwiązanie;
  • dwa różne rozwiązania
Wersja PDF

Rozwiązanie

Spróbujmy rozwiązać podane równanie

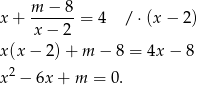
m − 8 x + ------= 4 / ⋅(x − 2 ) x − 2 x (x− 2)+ m − 8 = 4x− 8 2 x − 6x + m = 0.

Zanim zajmiemy się ustalaniem ile jest pierwiastków tego równania, sprawdźmy kiedy 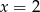x = 2 jest pierwiastkiem – musimy to wiedzieć, bo 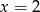x = 2 nie należy do dziedziny wyjściowego równania.

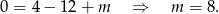
0 = 4 − 12 + m ⇒ m = 8.
  • Mamy dwie możliwości, albo powyższe równanie kwadratowe ma dwa pierwiastki i jeden z nich to 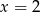x = 2 , albo równanie to ma jeden pierwiastek. Jak już wiemy, pierwszy warunek oznacza 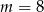m = 8 , pozostało sprawdzić kiedy Δ = 0 .
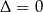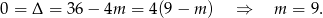
    0 = Δ = 36− 4m = 4(9 − m ) ⇒ m = 9.

     
    Odpowiedź: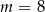 m = 8 lub m = 9

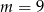
  • Wystrczy sprawdzić kiedy 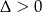Δ > 0 i wyrzucić przypadek m = 8 .
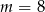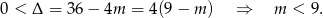
    0 < Δ = 36− 4m = 4(9 − m ) ⇒ m < 9.

     
    Odpowiedź: m ∈ (− ∞ ,8)∪ (8,9)

Wersja PDF