/Szkoła średnia/Równania/Z wartością bezwględną/Układy równań/Inne

Zadanie nr 6602196

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbadaj liczbę rozwiązań układu równań w zależności od parametru 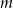m

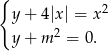
{ y + 4|x| = x 2 y + m 2 = 0.

Rozwiązanie

Rozwiązania danego układu równań to punkty wspólne wykresu funkcji 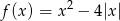f (x) = x2 − 4|x| oraz poziomej prostej 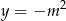y = −m 2 . Aby ustalić ile może być tych punktów wspólnych, szkicujemy wykres funkcji

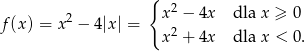
{ 2 x2 − 4x dla x ≥ 0 f(x ) = x − 4|x| = 2 x + 4x dla x < 0.

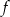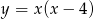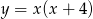Jak widać z powyższego wzoru, wykres funkcji f składa się z dwóch kawałków parabol y = x(x − 4) i y = x(x + 4) . Pierwsza z tych parabol ma wierzchołek w punkcie 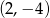(2,− 4) , a druga w punkcie 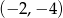(− 2,− 4) . Szkicujemy wykres.

PIC

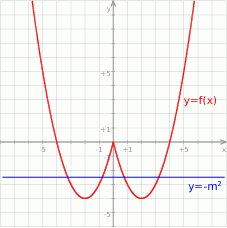
Z wykresu widać, że liczba rozwiązań układu równań jest równa

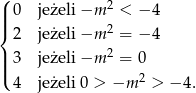
( 2 || 0 jeżeli −m < − 4 |{ 2 jeżeli −m 2 = − 4 2 ||| 3 jeżeli −m = 0 ( 4 jeżeli 0 > −m 2 > − 4.

Bardziej wprost, mamy

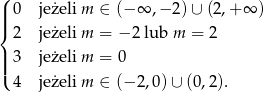
(| 0 jeżeli m ∈ (− ∞ ,− 2)∪ (2,+ ∞ ) ||{ 2 jeżeli m = − 2 lub m = 2 || 3 jeżeli m = 0 |( 4 jeżeli m ∈ (− 2,0)∪ (0 ,2).

 
Odpowiedź: ( | 0 je żeli m ∈ (− ∞ ,− 2) ∪ (2,+ ∞ ) ||{ 2 je żeli m = − 2 lub m = 2 || 3 je żeli m = 0 |( 4 je żeli m ∈ (− 2 ,0 )∪ (0,2).

Wersja PDF