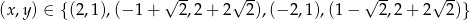/Szkoła średnia/Równania/Z wartością bezwględną/Układy równań/Inne/Rozwiąż układ

Zadanie nr 1059105

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż układ równań 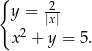{ -2- y = |x| x2 + y = 5.

Rozwiązanie

Sposób I

Podstawiając z pierwszego równania do drugiego mamy

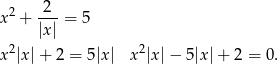
2 x2 + --- = 5 |x| x2|x|+ 2 = 5|x| x2|x|− 5 |x| + 2 = 0.

Jeżeli 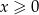x ≥ 0 to mamy rówanie

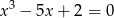
3 x − 5x + 2 = 0

Szukamy pierwiastków całkowitych – łatwo zauważyć, że pierwiastkiem jest 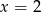x = 2 . Dzielimy przez 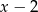x − 2 – my zrobimy to grupując wyrazy

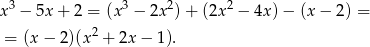
3 3 2 2 x − 5x+ 2 = (x − 2x )+ (2x − 4x )− (x− 2) = = (x− 2)(x2 + 2x − 1).

Szukamy pierwiastków trójmianu w nawiasie

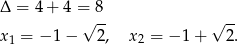
Δ = 4 + 4 = 8 √ -- √ -- x1 = − 1 − 2, x 2 = − 1+ 2.

Tylko drugi z tych pierwiastków jest nieujemny, mamy więc w tym przypadku dwa rozwiązania

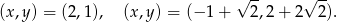
√ -- √ -- (x,y) = (2,1 ), (x,y) = (− 1 + 2,2 + 2 2 ).

Zajmijmy się teraz przypadkiem 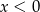x < 0 , czyli równaniem

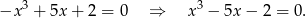
−x 3 + 5x + 2 = 0 ⇒ x3 − 5x − 2 = 0.

Tak jak poprzednio znajdujemy pierwiastek 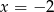x = − 2 i dzielimy przez (x + 2) .

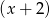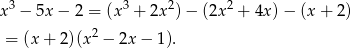
x3 − 5x − 2 = (x 3 + 2x 2)− (2x2 + 4x) − (x + 2) 2 = (x + 2)(x − 2x − 1 ).

Szukamy pierwiastków trójmianu w nawiasie.

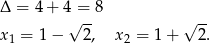
Δ = 4 + 4 = 8 √ -- √ -- x1 = 1 − 2, x 2 = 1+ 2.

Tylko pierwszy z pierwiastków jest ujemny. Mamy więc rozwiązania

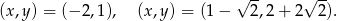
√ -- √ -- (x,y) = (− 2,1), (x,y) = (1 − 2,2 + 2 2 ).

Sposób II

Zadanie można rozwiązać odrobinę szybciej jeżeli zapiszemy wyjściowe równanie w postaci

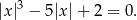
3 |x| − 5|x|+ 2 = 0.

Po podstawieniu 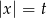|x| = t mamy równanie 3 stopnia

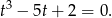
3 t − 5t+ 2 = 0.

Rozwiązaliśmy je już w poprzednim sposobie

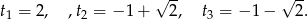
√ -- √ -- t1 = 2, ,t2 = − 1 + 2, t3 = − 1 − 2.

Ostatnie rozwiązanie odrzucamy, gdyż ma być 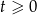t ≥ 0 . Łatwo stąd otrzymać 4 możliwe rozwiązania.  
Odpowiedź: √ -- √ -- √ -- √ -- (x ,y) ∈ {(2,1),(− 1 + 2,2 + 2 2),(− 2,1),(1 − 2,2 + 2 2 )}

Wersja PDF