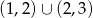/Szkoła średnia/Nierówności/Z wartością bezwzględną/Interpretacja geometryczna

Zadanie nr 1480509

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż graficznie nierówność 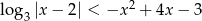2 log3 |x − 2 | < −x + 4x − 3 .

Rozwiązanie

Wykres prawej strony to parabola 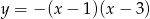y = − (x − 1)(x − 3 ) (liczymy z 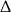Δ -y) o ramionach skierowanych w dół, miejscach zerowych 1 i 3 wierzchołku w punkcie (2,1) .

PIC

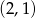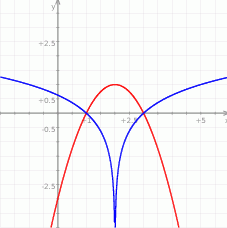
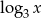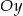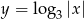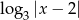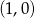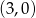Wykres prawej strony możemy otrzymać następująco: bierzemy dwie kopie wykresu log3x symetryczne względem osi Oy – to jest wykres funkcji y = lo g |x| 3 . Teraz przesuwamy ten wykres o dwie jednostki w prawo i mamy lo g3|x − 2| . Jeżeli naszkicujemy to w miarę dokładnie, to widać, że wykresy te przecinają się w dwóch punktach. Łatwo sprawdzić (ze wzoru), że te punkty to (1,0) i (3,0) . Zatem rozwiązaniem podanej nierówności jest zbiór 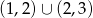(1,2) ∪ (2,3) (wyrzucamy 2, ze względu na dziedzinę logarytmu).  
Odpowiedź: (1,2) ∪ (2,3)

Wersja PDF