/Szkoła średnia/Funkcje - wykresy/Homografia/Różne

Zadanie nr 4609980

Dana jest funkcja 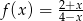2+x- f(x ) = 4−x , gdzie x ∈ R ∖ {4} .

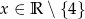  • Wyznacz wszystkie punkty należące do wykresu funkcji 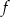f , których obie współrzędne są liczbami pierwszymi.
  • Podaj zbiór tych argumentów, dla których funkcja 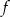f przyjmuje wartości nieujemne.
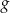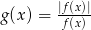  • Naszkicuj wykres funkcji g , jeśli |f(x)| g(x ) = -f(x)- .
PIC
Wersja PDF

Rozwiązanie

  • Przekształćmy wzór funkcji do postaci kanonicznej.
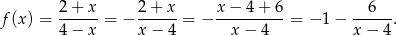
    f(x) = 2-+-x- = − 2-+-x-= − x-−-4-+-6-= −1 − --6--. 4 − x x − 4 x − 4 x− 4

    Jeżeli wartością funkcji 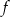f ma być liczba całkowita, to 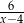-6-- x−4 musi być liczbą całkowitą, czyli 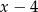x − 4 musi dzielić 6. Zatem 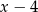x− 4 musi być jedną z liczb 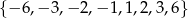{− 6 ,− 3 ,− 2 ,− 1 ,1,2,3,6} . To z kolei oznacza, że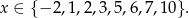

    x ∈ {− 2,1,2,3,5,6,7 ,10}.

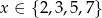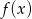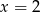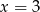    Ponieważ x ma być liczbą pierwszą, pozostają możliwości x ∈ {2,3 ,5 ,7} . Dla każdej z tych wartości liczymy f (x) i sprawdzamy, czy wychodzi liczba pierwsza. Gdy to zrobimy okaże się, że liczbę pierwszą otrzymujemy tylko dla x = 2 i x = 3 . Dla tych wartości otrzymujemy punkty wykresu: 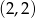(2,2) i (3,5 ) .  
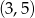    Odpowiedź: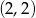 (2,2) i (3,5)

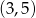
  • Rozwiązujemy nierówność
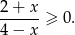
    2+ x 4−-x--≥ 0.

    Oczywiście musimy założyć, że 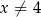x ⁄= 4 . Przy tym założeniu powyższa nierówność jest równoważna nierówności kwadratowej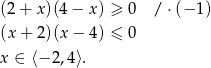

    (2 + x)(4 − x) ≥ 0 / ⋅(− 1) (x + 2)(x − 4) ≤ 0 x ∈ ⟨− 2,4⟩.

    Na koniec wyrzucamy z tego zbioru x = 4 .  
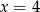    Odpowiedź: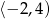 ⟨− 2,4)

  • Korzystając z poprzedniego podpunktu mamy
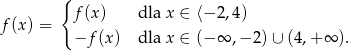
    { f(x) dla x ∈ ⟨− 2,4) f(x) = −f (x) dla x ∈ (− ∞ ,− 2) ∪ (4,+ ∞ ).

    Zatem

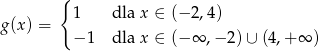
    { g(x) = 1 dla x ∈ (− 2,4) −1 dla x ∈ (− ∞ ,− 2)∪ (4,+ ∞ )

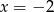    (x = − 2 nie należy do dziedziny funkcji 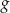g , bo f (− 2) = 0 ).

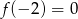    Teraz bez trudu szkicujemy wykres.

    PIC
Wersja PDF