/Szkoła średnia/Funkcje - wykresy/Homografia/Różne

Zadanie nr 4833526

Dodaj do ulubionych
Dodaj do rozwiązanych

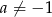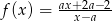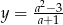Wyznacz wszystkie wartości parametru a ⁄= −1 , dla których wykres funkcji f (x) = ax+x2−aa−-2 nie ma punktów wspólnych z prostą 2 y = aa−+31 .

Rozwiązanie

Sposób I

Pytanie postawione w treści zadania to skomplikowany sposób zapytania o to, kiedy równanie

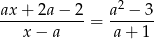
2 ax-+--2a−--2 = a--−-3 x− a a+ 1

nie ma rozwiązań. Przekształcamy to równanie

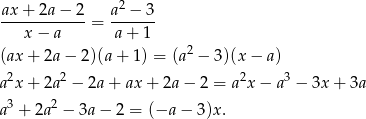
2 ax-+-2a-−-2-= a--−-3 x − a a+ 1 (ax + 2a − 2)(a + 1) = (a2 − 3)(x − a ) a2x + 2a2 − 2a + ax + 2a − 2 = a2x− a3 − 3x+ 3a 3 2 a + 2a − 3a− 2 = (−a − 3)x.

Widać teraz gołym okiem, że równanie jest sprzeczne dla 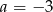a = − 3 . Jeżeli 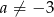a ⁄= − 3 to równanie ma dokładnie jedno rozwiązanie 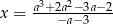x = a3+2a2−3a−2 −a −3 . To jednak nie koniec! – musimy jeszcze sprawdzić, czy to rozwiązanie na pewno jest w dziedzinie funkcji 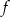f , czyli sprawdzamy kiedy

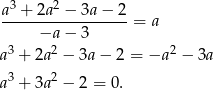
a3 + 2a 2 − 3a − 2 -----------------= a −a − 3 a3 + 2a2 − 3a − 2 = −a 2 − 3a 3 2 a + 3a − 2 = 0.

Łatwo zauważyć, ze jednym z pierwiastków tego równania jest 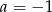a = − 1 . Dzielimy więc prawą stronę równania przez 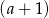(a+ 1) – my zrobimy to grupując wyrazy.

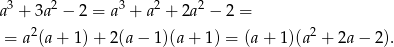
a3 + 3a2 − 2 = a3 + a2 + 2a2 − 2 = 2 2 = a (a + 1) + 2(a − 1)(a + 1) = (a + 1)(a + 2a − 2).

Pozostało teraz rozłożyć trójmian w nawiasie.

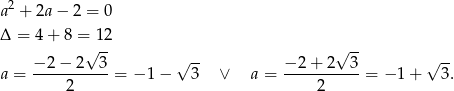
2 a + 2a − 2 = 0 Δ = 4+ 8 = 12 √ -- √ -- −2-−-2---3- √ -- −-2+--2--3- √ -- a = 2 = − 1 − 3 ∨ a = 2 = − 1 + 3.

Sposób II

Przekształćmy wzór funkcji 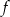f tak, aby było widać jaka jest asymptota pozioma.

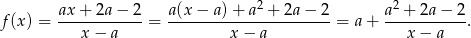
2 2 f(x) = ax-+-2a-−-2-= a(x−--a)+--a-+--2a−--2-= a + a--+-2a-−-2-. x − a x − a x − a

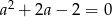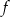Widać, że mamy teraz dwie możliwości: jeżeli a2 + 2a − 2 = 0 to f jest funkcją liniową 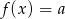f(x) = a , a w przeciwnym przypadku 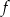f jest funkcją homograficzną z asymptotą poziomą 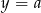y = a . Sprawdźmy kolejno te możliwości.

Funkcja 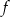f jest liniowa jeżeli

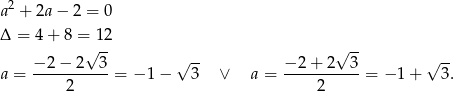
a2 + 2a − 2 = 0 Δ = 4+ 8 = √12 √ -- −2 − 2 3 √ -- − 2+ 2 3 √ -- a = -----------= − 1 − 3 ∨ a = -----------= − 1 + 3. 2 2

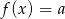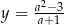Musimy jeszcze sprawdzić, czy w tym przypadku rzeczywiście proste f (x) = a i y = a2−-3 a+1 są rozłączne. Sprawdzamy

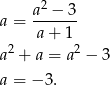
a2 −-3 a = a + 1 2 2 a + a = a − 3 a = − 3.

Otrzymana wartość nie jest równa wcześniej otrzymanym wartościom 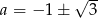√ -- a = −1 ± 3 , więc proste rzeczywiście są rozłączne.

Zajmijmy się teraz przypadkiem funkcji homograficznej z asymptotą poziomą 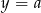y = a . W takiej sytuacji wykres funkcji 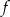f będzie rozłączny z podaną prostą dokładnie wtedy, gdy ta prosta będzie się pokrywać z asymptotą, tzn. gdy

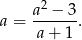
a2 − 3 a = ------. a + 1

Jak widzieliśmy przed chwilą rozwiązaniem tego równania jest 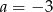a = − 3 .  
Odpowiedź: √ -- √ -- a ∈ {− 3,− 1 − 3,− 1 + 3}

Wersja PDF