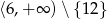/Szkoła średnia/Funkcje - wykresy/Wymierny/Różne

Zadanie nr 2544449

Dodaj do ulubionych
Dodaj do rozwiązanych

Określ dziedzinę funkcji 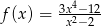3x4−-12- f(x) = x2− 2 i sprowadź jej wzór do najprostszej postaci. Naszkicuj jej wykres i podaj jej zbiór wartości.

Rozwiązanie

Dziedziną jest oczywiście zbiór 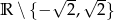√ --√ -- R ∖{ − 2, 2} (wyrzucamy zera mianownika). Przekształćmy wzór funkcji.

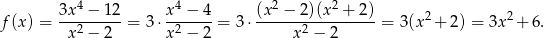
4 4 2 2 f(x) = 3x--−-12-= 3⋅ x-−-4-= 3⋅ (x-−--2)(x-+--2)-= 3(x 2+ 2) = 3x 2+ 6 . x2 − 2 x 2 − 2 x2 − 2

Bez trudu rysujemy wykres – jest to parabola 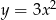y = 3x2 przesunięta o 6 jednostek w górę. Jedyna rzecz, na którą trzeba uważać, to fakt, że z dziedziny funkcji są usunięte liczby 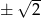√ -- ± 2 – oznaczyliśmy to dziurami na wykresie w punktach √ -- (± 2,1 2) .

PIC

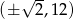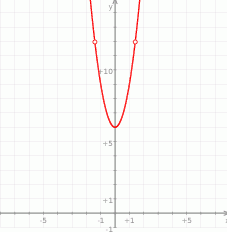
Zbiór wartości odczytujemy z wykresu: 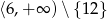⟨6 ,+ ∞ ) ∖{ 12} .  
Odpowiedź: 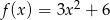f(x ) = 3x2 + 6 , dziedzina: 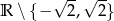R ∖{− √ 2-,√ 2} , zbiór wartości: ⟨6,+ ∞ )∖ {12 }

Wersja PDF