/Szkoła średnia/Ciągi/Arytmetyczny/Na dowodzenie

Zadanie nr 1600989

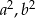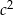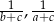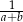Wykaż, że jeżeli liczby 2 2 a ,b i 2 c tworzą ciąg arytmetyczny, który nie jest stały, to liczby b+1c-,a1+c- i a+1b- również tworzą ciąg arytmetyczny.

Wersja PDF

Rozwiązanie

Wiemy, że 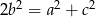2 2 2 2b = a + c , a mamy wykazać, że

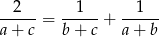
2 1 1 ----- = -----+ ------ a + c b+ c a+ b

Przekształćmy tę równość.

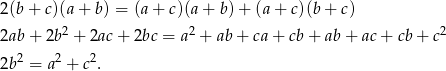
2 (b+ c)(a + b) = (a+ c)(a + b) + (a + c)(b + c) 2ab + 2b2 + 2ac+ 2bc = a2 + ab + ca+ cb+ ab+ ac+ cb+ c2 2 2 2 2b = a + c .

Otrzymaliśmy równość, o której wiemy, że jest prawdziwa. Prawdziwa jest więc też równość od której zaczęliśmy.

Wersja PDF