Zadanie nr 2919461
Sześcian największej z czterech różnych liczb całkowitych, tworzących rosnący ciąg arytmetyczny o wyrazach dodatnich, jest równy sumie sześcianów pozostałych liczb. Wykaż, że iloczyn dwóch z tych liczb jest o 60% większy od iloczynu dwóch pozostałych.
Rozwiązanie
Jeżeli oznaczymy kolejne wyrazy ciągu, o którym mowa w treści zadania przez 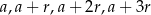 , to największym wyrazem tego ciągu jest
, to największym wyrazem tego ciągu jest 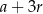 i wiemy, że liczby te spełniają warunek
i wiemy, że liczby te spełniają warunek
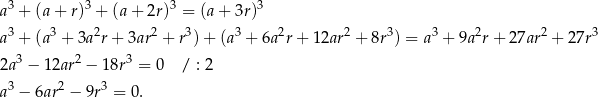
Otrzymane równanie rozwiążemy na dwa sposoby.
Sposób I
Wiemy, że ciąg jest rosnący, więc 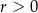 . Podzielmy otrzymane równanie przez
. Podzielmy otrzymane równanie przez 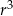 .
.
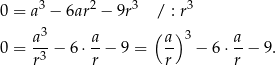
Podstawmy teraz 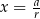 .
.
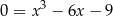
Szukamy pierwiastków całkowitych tego równania – sprawdzamy dzielniki wyrazu wolnego. Jednym z pierwiastków jest 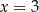 , więc dzielimy wielomian z prawej strony przez
, więc dzielimy wielomian z prawej strony przez 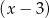 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
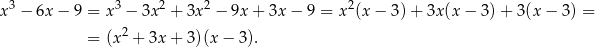
Trójmian w pierwszym nawiasie nie ma pierwiastków, bo 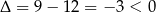 . Zatem
. Zatem
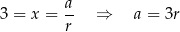
i dany ciąg to
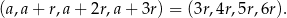
W szczególności
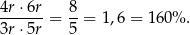
To oznacza, że iloczyn 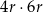 jest o 60% większy od iloczynu
jest o 60% większy od iloczynu 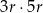 .
.
Sposób II
Jeżeli równanie potraktujemy jak równanie zmiennej  z parametrem
z parametrem  , to ewentualnych rozwiązań szukamy wśród dzielników wyrazu wolnego
, to ewentualnych rozwiązań szukamy wśród dzielników wyrazu wolnego 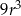 . Widać też, że rozwiązanie musi zawierać
. Widać też, że rozwiązanie musi zawierać  (bo inaczej nie wyzerują się składniki z
(bo inaczej nie wyzerują się składniki z  ). Najprostsze dzielniki wyrazu wolnego tej postaci to
). Najprostsze dzielniki wyrazu wolnego tej postaci to 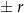 i
i 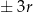 . Sprawdzając po kolei możemy zauważyć, że równanie jest spełnione przez
. Sprawdzając po kolei możemy zauważyć, że równanie jest spełnione przez 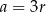 – mamy wtedy
– mamy wtedy
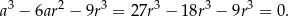
Dzielimy teraz równanie przez 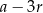 , my zrobimy to grupując wyrazy.
, my zrobimy to grupując wyrazy.
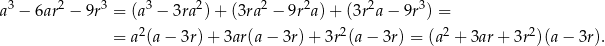
Liczymy jeszcze 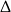 –ę trójmianu w pierwszym nawiasie.
–ę trójmianu w pierwszym nawiasie.
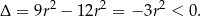
W takim razie jedyna możliwość to 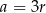 . Dalszy ciąg rozwiązania przeprowadzamy tak samo, jak w poprzednim sposobie.
. Dalszy ciąg rozwiązania przeprowadzamy tak samo, jak w poprzednim sposobie.

