/Szkoła średnia/Ciągi/Arytmetyczny/Na dowodzenie

Zadanie nr 4578986

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja określona wzorem 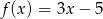f(x) = 3x − 5 .

  • Wyznacz ogólny wyraz ciągu 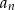an wiedząc, że: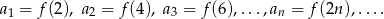
    a1 = f(2), a 2 = f(4), a3 = f(6),...,an = f(2n),....
  • Uzasadnij, że ciąg 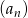(an) jest ciągiem arytmetycznym.
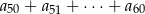  • Oblicz sumę a50 + a51 + ⋅ ⋅⋅+ a60 .

Rozwiązanie

  • Liczymy
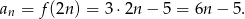
    an = f(2n ) = 3 ⋅2n − 5 = 6n − 5.

     
    Odpowiedź: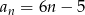 an = 6n − 5

  • Możemy skorzystać, ze wzoru na wyraz ogólny ciągu arytmetycznego i wtedy widać, że ciąg
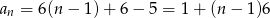
    an = 6 (n − 1)+ 6− 5 = 1+ (n − 1)6

    jest ciągiem arytmetycznym o pierwszym wyrazie 1 i różnicy 6.

    Możemy też sprawdzić wprost, że różnica między dwoma kolejnymi wyrazami ciągu jest stała (tzn. nie zależy od n ).

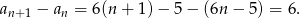
    an+ 1 − an = 6(n + 1) − 5− (6n − 5) = 6 .
  • Korzystamy ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego.
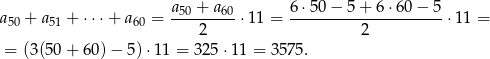
    a + a + ⋅ ⋅⋅+ a = a50-+-a60-⋅11 = 6⋅5-0−-5-+-6-⋅60-−-5-⋅11 = 50 51 60 2 2 = (3(50 + 6 0)− 5 )⋅11 = 325 ⋅11 = 357 5.

     
    Odpowiedź: 3575

Wersja PDF