Zadanie nr 5478645
Dwie dowolne liczby rzeczywiste i ich suma tworzą ciąg arytmetyczny (niekoniecznie w takiej kolejności). Wykaż, że jedna z tych liczb jest dwukrotnością drugiej liczby lub, że liczby te są liczbami przeciwnymi.
Rozwiązanie
Suma dwóch danych liczb może być ustawiona z nimi w ciąg arytmetyczny na 3 sposoby (na początku, w środku , lub na końcu). Mamy w takim razie do rozpatrzenia 3 przypadki.
Jeżeli ciąg 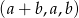 jest arytmetyczny, to
jest arytmetyczny, to
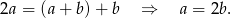
Jeżeli ciąg 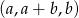 jest arytmetyczny, to
jest arytmetyczny, to
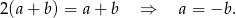
Jeżeli ciąg 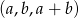 jest arytmetyczny, to
jest arytmetyczny, to