Zadanie nr 5813879
Ciągi 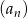 i
i 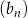 , gdzie
, gdzie 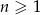 są ciągami arytmetycznymi. Wykaż, że jeżeli ciąg
są ciągami arytmetycznymi. Wykaż, że jeżeli ciąg 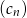 zdefiniowany wzorem
zdefiniowany wzorem 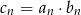 (
(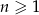 ) jest ciągiem arytmetycznym, to różnica jednego z ciągów
) jest ciągiem arytmetycznym, to różnica jednego z ciągów 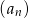 lub
lub 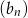 jest równa zeru.
jest równa zeru.
Rozwiązanie
Sposób I
Niech 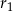 i
i 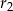 będą różnicami odpowiednio ciągów
będą różnicami odpowiednio ciągów 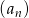 i
i 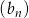 , tzn.
, tzn.
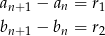
dla 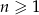 . Wiemy, że ciąg
. Wiemy, że ciąg 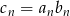 też jest arytmetyczny, więc dla dowolnego
też jest arytmetyczny, więc dla dowolnego 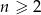 mamy
mamy
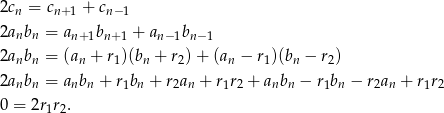
Zatem rzeczywiście 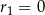 lub
lub 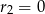 .
.
Sposób II
Ciągi arytmetyczne to ciągi mające wzór postaci 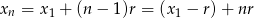 . Wiemy zatem, że
. Wiemy zatem, że
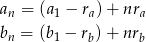
dla pewnych liczb 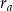 i
i 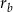 . Wtedy
. Wtedy
![cn = anbn = ((a1 − ra)+ nra)((b1 − rb)+ nrb ) = 2 = [(a1 − ra)(b1 − rb)]+ n [ra(b1 − rb)+ rb(a1 − ra)]+ n rarb.](https://img.zadania.info/zad/5813879/HzadR15x.gif)
Jeżeli ciąg ten jest ciągiem arytmetycznym, to współczynnik przy 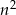 musi być równy 0. Zatem
musi być równy 0. Zatem 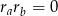 , czyli
, czyli 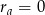 lub
lub 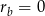 .
.

