Zadanie nr 7815790
Ciąg 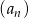 dla
dla 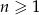 jest ciągiem arytmetycznym oraz
jest ciągiem arytmetycznym oraz 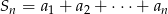 dla
dla 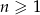 . Wykaż, że jeżeli spełniony jest warunek
. Wykaż, że jeżeli spełniony jest warunek 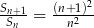 dla
dla 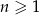 , to spełniony jest również warunek
, to spełniony jest również warunek 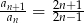 .
.
Rozwiązanie
Sposób I
Korzystamy ze wzoru 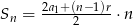 na sumę kolejnych wyrazów ciągu arytmetycznego.
na sumę kolejnych wyrazów ciągu arytmetycznego.
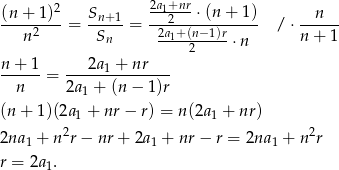
Ze wzoru na  -ty wyraz ciągu arytmetycznego mamy więc
-ty wyraz ciągu arytmetycznego mamy więc
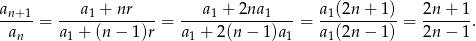
Sposób II
Korzystamy ze wzoru 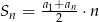 na sumę kolejnych wyrazów ciągu arytmetycznego.
na sumę kolejnych wyrazów ciągu arytmetycznego.
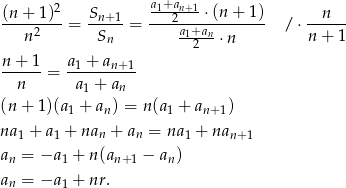
Z drugiej strony wiemy, że 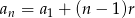 . Mamy zatem równanie
. Mamy zatem równanie
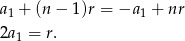
Ciąg 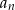 jest więc ciągiem arytmetycznym o różnicy
jest więc ciągiem arytmetycznym o różnicy 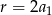 . Stąd
. Stąd
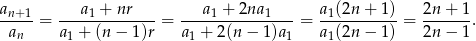
Sposób III
Skoro dany warunek
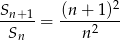
jest spełniony dla dowolnej liczby naturalnej  , możemy w nim podstawić
, możemy w nim podstawić 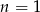 .
.
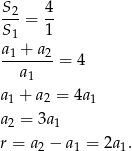
Ciąg 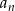 jest więc ciągiem arytmetycznym o różnicy
jest więc ciągiem arytmetycznym o różnicy 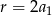 . Stąd
. Stąd