Zadanie nr 8406564
Ciągi 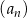 i
i 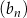 , gdzie
, gdzie 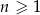 , są ciągami arytmetycznymi. Ciąg
, są ciągami arytmetycznymi. Ciąg 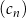 jest określony wzorem
jest określony wzorem 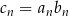 , dla
, dla 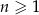 , a ciąg
, a ciąg 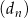 ciągiem różnic dwóch kolejnych wyrazów ciągu
ciągiem różnic dwóch kolejnych wyrazów ciągu 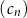 :
: 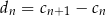 , dla
, dla 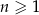 . Wykaż, że ciąg
. Wykaż, że ciąg 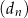 jest ciągiem arytmetycznym, którego różnica jest równa podwojonemu iloczynowi różnic ciągów
jest ciągiem arytmetycznym, którego różnica jest równa podwojonemu iloczynowi różnic ciągów 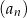 i
i 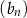 .
.
Rozwiązanie
Niech 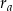 i
i 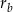 będą różnicami odpowiednio ciągów
będą różnicami odpowiednio ciągów 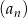 i
i 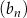 , tzn.
, tzn.
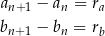
dla 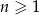 . Mamy wtedy
. Mamy wtedy
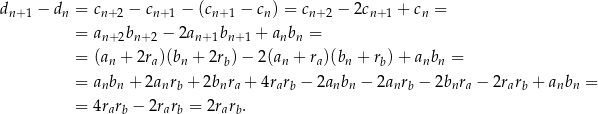
To dowodzi, że rzeczywiście ciąg 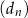 jest ciągiem arytmetycznym o różnicy
jest ciągiem arytmetycznym o różnicy 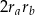 .
.

