Punkty A,B należą do jednego ramienia kąta o wierzchołku O, a... Zadania.info: rozwiązanie zadania, Różne, 4529519

Zadania.info

Największy internetowy zbiór zadań z matematyki

Rejestracja

Forum

Szukaj

Pomoc

Baza zawiera: 17735 zadań, 1024 zestawy, 35 poradników

cornersUpL

cornersUpR

random

Linki sponsorowane

cornersR

/Szkoła średnia/Geometria/Planimetria/Różne

Zadanie nr 4529519

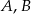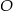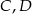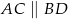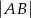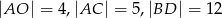Punkty $A ,B$ należą do jednego ramienia kąta o wierzchołku $O$ , a punkty $C ,D$ należą do jego drugiego ramienia i wiadomo, że $AC ∥ BD$ . Wyznacz $|AB |$ , jeśli wiadomo, że $|AO | = 4,|AC | = 5,|BD | = 12$ .

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku

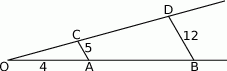
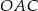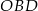Oczywiście trójkąty $OAC$ i $OBD$ są podobne zatem

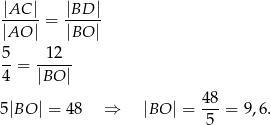
|AC--|-= |BD-| |AO | |BO | 5 12 --= ----- 4 |BO | 48- 5 |BO | = 4 8 ⇒ |BO | = 5 = 9,6.

Stąd

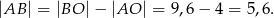
|AB | = |BO |− |AO | = 9,6− 4 = 5,6.

Odpowiedź: $|AB | = 5,6$

Wersja PDF

Twoje uwagi

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz

Legalni bukmacherzy