Zadanie nr 2571010
Wykaż, że jeżeli ciąg 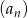 jest ciągiem geometrycznym o wyrazach dodatnich, to ciąg o wyrazie ogólnym
jest ciągiem geometrycznym o wyrazach dodatnich, to ciąg o wyrazie ogólnym 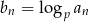 , dla
, dla 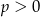 i
i 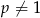 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Rozwiązanie
Sposób I
Musimy sprawdzić, czy różnica dwóch kolejnych wyrazów ciągu 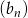 jest stała, tzn. nie zależy od
jest stała, tzn. nie zależy od  . Liczymy
. Liczymy
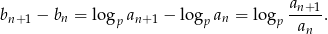
Ostatnia liczba nie zależy od  , bo
, bo 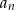 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
Sposób II
Ze wzoru na  –ty wyraz ciągu geometrycznego mamy
–ty wyraz ciągu geometrycznego mamy 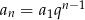 , gdzie
, gdzie 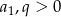 . Zatem
. Zatem
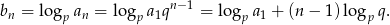
Widać teraz, że 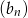 jest ciągiem arytmetycznym o pierwszym wyrazie
jest ciągiem arytmetycznym o pierwszym wyrazie 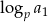 i różnicy
i różnicy 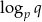 .
.

