Zadanie nr 6573005
Udowodnij, że jeżeli ciąg 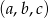 jest jednocześnie arytmetyczny i geometryczny to
jest jednocześnie arytmetyczny i geometryczny to 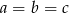 .
.
Rozwiązanie
Sposób I
Wiemy, że 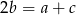 i
i 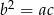 . Podstawiając z pierwszego równania do drugiego za
. Podstawiając z pierwszego równania do drugiego za 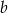 mamy
mamy
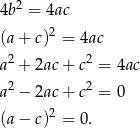
Zatem  . Mamy więc
. Mamy więc 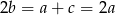 , czyli
, czyli 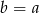 .
.
Sposób II
Ponieważ 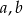 i
i  tworzą ciąg geometryczny, to
tworzą ciąg geometryczny, to 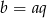 i
i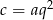 . Mamy wtedy
. Mamy wtedy
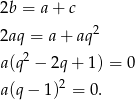
Zatem 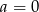 lub
lub 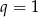 . Każdy z warunków oznacza, że
. Każdy z warunków oznacza, że 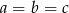 .
.
Sposób III
Ponieważ liczby 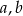 i
i  tworzą ciąg arytmetyczny, więc
tworzą ciąg arytmetyczny, więc 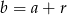 ,
, 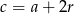 . Mamy wtedy
. Mamy wtedy
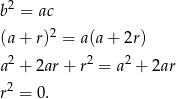
Zatem 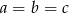 .
.

